Clément Canonne

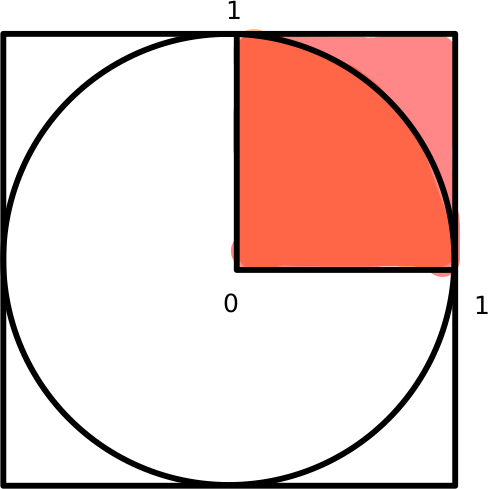
Code 1: looking at plop(), we see that x,y are independent uniform random variables in [0,1], and we return 1 if the vector (x,y) has Euclidean norm at most 1. What is the probability that this happens? We’re picking a point uniformly in the top right square, which has area 1, and looking at the probability to land into the circle (of radius r=1), whose intersection with that square is a fourth of the total circle area, so πr²/4 = π/4.

def plop():
    (x,y) = rng.random(2) 
    return int(x**2+y**2 <= 1)
def plops(n): # First thing
    return sum([4*plop()/n for _ in range(n)])

So each draw of plop() is 1 with probability π/4: plops() then computes the empirical mean of n such independent draws, multiplies it by 4, and… we get something whose expected value is π/4×4=π 🥧! Moreover, since we’re basically looking at the empirical mean of a bunch of independent Bernoulli random variables (a.k.a. a (scaled) Binomial), we get by Hoeffding/Chernoff bounds that this converges to π really fast.

Code 2: fleb() picks an integer between 1 and n uniformly at random, and returns 1 if it’s prime. What is the probability that this happens? It’s entirely obvious, but the Prime Number Theorem (PNT) guarantees that, as n goes to infinity, this behaves as 1/ln(n). More precisely, if π(n) (Yes, π… but not that π 🥧!) denotes the number of prime numbers in {1,..,n}, then the PNT states that \(\frac{\pi(n) \ln n}{n} \rightarrow 1\)

which justifies what our code is trying to do.

def fleb(n):
    x = rng.integers(1,n+1)
    return int(is_prime(x))
def flebs(n): # Second thing
    return sum([fleb(n+1)*np.log(n+1)/n for _ in range(n)])

How fast does it get there? It doesn’t say 🤷. But “we” [not me] can get quantitative bounds, and it gets there quite fast: https://en.wikipedia.org/wiki/Prime_number_theorem#Non-asymptotic_bounds_on_the_prime-counting_function Now, what does flebs() do? Given a (large enough?) n, it tries to estimate that probability to be prime, $\frac{\pi(n+1)}{n+1}$, by random sampling (again, empirical mean of a bunch of Bernoulli… using n+1 instead of n for no particularly good reason) It does that for n attempts, takes the average, and voilà! A very good estimate of the constant… 1. (It converges, again, very fast! To 1. 🧐)

💡 Note that there is no particular reason to use the same n for both the “large number in fleb() and the number of repetitions to do the statistical estimate. They are absolutely not tied to each other, but that quiz didn’t try not to confuse you 🙃. To be more precise, for a given n, each call to fleb(n+1) is a Bernoulli with parameter $\frac{\pi(n+1)}{n+1}\approx 1/\ln n$ (this is what we are trying to estimate), and so also with variance $\sigma^2 \approx 1/\ln n$. If we were to take the empirical mean over $N$ repetitions, we’d get an estimator with variance $\sigma^2/N \approx 1/(N\ln n)$, so we expect it to oscillate around its mean by a few standard deviations, so $O(1/\sqrt{N\log n})$. For our choice of $N=n$, that gives an estimate of $\frac{\pi(n+1)}{n+1}$ within $\pm O(1/\sqrt{n\log n})$, so an estimate of $1$ within $\pm O(\sqrt{\log n/n})$.

Code 3: Oh, I like that one, and it’s not the first time I mentioned it!. There is a very nice probability fact, which has a very easy heuristic but “wrong” proof (and a not-so-easy correct one to make it formal) which states that the probability \(p_n = \Pr[ \text{gcd}(x,y) = 1 ]\) that two independent and uniformly random integers in {1,..,n} are coprime goes to 6/π² as n grows. So blah(), armed with that fact, picks two such integers, and returns 1 iff they are coprime, proudly returning a Bernoulli r.v. with parameter $p_n$.

def blah(n):
    (x,y) = rng.integers(1,n+1, size=2)
    return int(np.gcd(x,y) == 1)
def blahs(n):  # Third thing
    return np.sqrt(6.0/sum([blah(n)/n for _ in range(n)]))

Then blahs() does that a bunch of time and takes the empirical mean (again using for not particular reason the same number n for “large integer” and “number of experiments to get a good estimate”: I didn’t try to make your task easy! 👀), thus estimating $p_n$ to accuracy roughly O(1/√n). Which results, fingers crossed, to a good estimate of 6/π² as well: the hope being that “estimate ≈ $p_n$ ≈ 6/π²”.

And then… we take the inverse of our estimate, multiply it by 6, take the square root, and tadam! An estimate of π 🥧!

Code 4: Ah, meeps(). What does it do? Surprise: it estimates π 🥧, again – but very badly! Basically, meep(n) generates a uniformly random $2n$-bit string $x$, and returns 1 iff $x$ has exactly $n$ bits set to $1$ (that is, has Hamming weight $n$).

def meep(n):
    x = rng.integers(2, size=2*n)
    return int(sum(x) == n)
def meeps(n):  # Fourth thing
    return 1/(n*sum([meep(n)/n for _ in range(n)])**2)

What’s the probability that this happens? Exactly the probability that a Binomial r.v. $X$ with parameters $2n$ and $1/2$ is equal to $n$, \(\Pr[X = n] = \binom{2n}{n}\frac{1}{2^{2n}}\) That… does not look to great, does it? Fortunately, using Stirling’s approximation, we get that for large $n$ \(\Pr[X = n] = \frac{(2n)!}{2^{2n}(n!)^2}\sim \frac{1}{\sqrt{\pi n}}\) Also, that approximation is really, really good. So again, meeps() calls meep() n times, takes the inverse, multiplies by n and squares the whole thing to go from an estimate of $\frac{1}{\sqrt{\pi n}}$ to an estimate of 🥧. But then why is the result so bad, if Stirling’s approximation is so good? 🤔

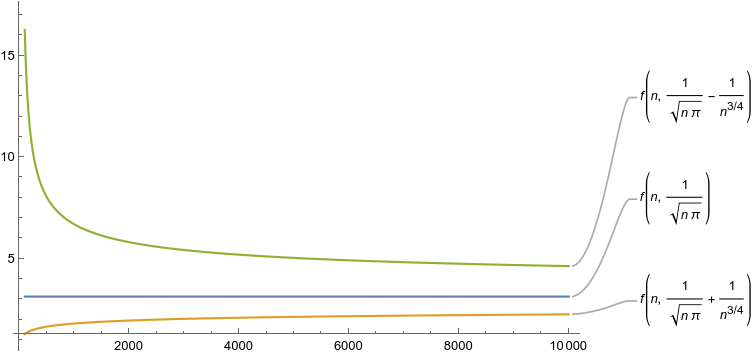
Let’s look at the quality of our estimate, when for a fixed n we take the sample mean over N repetitions (for us, N=n, but again — that’s arbitrary). By the above, we estimate the parameter $p_n$ of a Bernoulli, which is approximately $\frac{1}{\sqrt{\pi n}}$, and so has variance $\sigma^2 \approx \frac{1}{\sqrt{\pi n}}$ as well. We end up with a sample mean with mean variance $\sigma^2/N = \Theta(1/(\sqrt{n}N))$, which for $N=n$ is $\Theta(1/n^{3/2})$. The estimator will fluctuate by something of the order of a standard deviation around its mean, so we’ll get \(\frac{1}{\sqrt{\pi n}} \pm \Theta( \frac{1}{n^{3/4}} )\) Still, it’s big, but not too bad, right? Err…. we’re not done. Once we have that estimate $\hat{p}_n$ of our parameter $p_n$, we want to extract the value of $\pi$, so we apply the function $f(x) = \frac{1}{nx^2}$ to $\hat{p}_n$. And that’s… not great! A Taylor series approximation shows that \(f(\frac{1}{\sqrt{\pi n}}\pm \frac{1}{n^{3/4}}) \approx \pi \pm \frac{2\pi^{3/2}}{n^{1/4}}\) so now we have an error of the order $\Theta(1/n^{1/4})$ around our estimate of $\pi$, not something behaving as $1/\sqrt{n}$ or so like for the others! 😬

Code 5: I like blop(). It chooses a uniformly random permutation π of {1,2,…,n} (no, nope, not that π!), and then counts the number of fixed points of π, that is how many i such that π(i)=i. Then it returns 1 if, and only if, there is no fixed point.

def blop(n):
    p = rng.permutation(n)
    return int( sum([ int(i==p[i]) for i in range(n) ]) == 0 )
def blops(n):  # Fifth thing
    return 1.0/sum([blop(n)/n for _ in range(n)])

So what is this supposed to do? Here’s a fun fact: as n goes to ∞, the number of fixed points of a uniformly random permutation converges to the Poisson distribution with parameter λ=1. (Fun exercise: proving that the expected number of fixed points is 1 is very easy, and a nice exercise). So What does that imply? That tells us that the probability to have 0 fixed points should converge to $e^{-1}$. which is the probability that a Poisson(1) r.v. equals 0! And yes: blops() calls blop() many times, uses that to get an estimate of $1/e$, then takes the inverse to estimate Euler’s number, $e$.